UNIVERSIDAD NACIONAL DE
COSTA RICA
Ingeniería en Topografía Catastro y
Geodesia
Curso: Geodesia Satélital
Tema: Practica #2
Profesor(a):
Ign: Gabriela Cordero
Estudiantes:
Adriana Chaves
Luis Montero
Leonel Potoy
UNIVERSIDAD NACIONAL DE
COSTA RICA
Ingeniería en Topografía Catastro y
Geodesia
Curso: Geodesia Satélital
Tema: Practica #2
Profesor(a):
Ign: Gabriela Cordero
Estudiantes:
Adriana Chaves
Luis Montero
Leonel Potoy
Práctica 2
Objetivos:Conocer los diferentes tipos de órbitas así como sus parámetros y formas de calcularlas.
1) Investigue los siguientes conceptos:
Órbita retrograda
MEO: Medium Earth Orbit
GEO: Geoestationary Orbit
2) Investigue que son los sistemas denominados SBAS
Órbitas Polares
Órbita que pasa por encima de los polos de un planeta o muy
cerca de ellos, es decir la inclinación de la órbita es cercana a los 90
grados. Un satélite en órbita polar pasa sobre cada punto del planeta cuando
éste gira sobre su eje.
Las órbitas polares se utilizan principalmente para la
tele detección desde el espacio para estudiar y controlar los recursos naturales
de la Tierra, estudiar la dinámica de procesos y fenómenos naturales, recopilar
información sobre el estado de los territorios en la superficie del planeta.
Por este motivo tiene utilidad tanto militar, satélites de reconocimiento, como
civil: científicos (como el estudio de la atmósfera), agrícolas, así como para
algunos satélites meteorológicos.
La constelación de satélites Iridium también utiliza una
órbita polar para proporcionar servicios de telecomunicaciones. Otra aplicación
son los satélites de salvamento marítimo Cospas-Sarsat.
Estos satélites operan en una órbita sincronizada con el
sol. El satélite pasa cada día el ecuador y cada latitud a la misma hora solar
local, lo cual quiere decir que el satélite pasa por encima de nuestras cabezas
a la misma hora solar a lo largo de todas las estaciones del año. Esta
característica permite la recogida regular de datos en horas consistentes, así
como comparaciones a largo plazo. El plano orbital de una órbita sincronizada
con el sol debe también rotar aproximadamente un grado al día para mantenerse
con respecto a la Tierra.
Órbitas
Geoestacionarias
Una órbita geoestacionaria (GEO = geosincronizada) es
aquella en la que el satélite siempre está en la misma posición con respecto a
la Tierra (que rota).
El satélite órbita a una altura de aproximadamente 35790 Km.
porque esto hace que el periodo orbital (la duración de una órbita) sea igual
al periodo de rotación de la Tierra (23h 56m 4.09s). Al orbitar al mismo ritmo
y en la misma dirección que la Tierra, el satélite esta estacionario
(sincronizado con respecto a la rotación de la Tierra).
Los satélites geoestacionarios proporcionan un panorama de
observación muy amplio permitiendo estudiar eventos meteorológicos. Esto es
especialmente útil para observar tormentas locales severas y ciclones
tropicales.
Órbita retrograda
Órbita de un satélite tal que la proyección del centro de
masas del satélite sobre el plano fundamental gira en sentido contrario que el
cuerpo principal alrededor de su eje.
LEO: Low Earth Orbit.
Comúnmente conocida como "órbita baja", es una
amplia franja orbital que se sitúa entre los 160 Km de altura y los 2000 Km de
altura.
Como la velocidad orbital es mayor cuanto más baja sea la
órbita, los objetos situados en esta franja se mueven a gran velocidad respecto
de la superficie terrestre, cubriendo una órbita completa en minutos o pocas
horas.
La desventaja es que, como están "rozando" las
capas exteriores de la atmósfera terrestre, tienen un rápido decaimiento
orbital y necesitan ser re posicionados con frecuencia para devolverlos a la
altura orbital correcta.
Es la clase de órbita circular donde se encuentra la Estación
Espacial Internacional, la gran mayoría de los satélites meteorológicos o de
observación, y muchos satélites de comunicaciones.
Principales aplicaciones: comunicaciones, espionaje y
tele detección. La nueva generación de low flyers son pequeños LEO, principalmente
para comunicaciones de datos que incluyen correo electrónico y paginación;
grandes LEOs, que permiten la red mundial de telefonía móvil; y LEO de banda
ancha, que ofrecen comunicaciones de datos de alta velocidad y alto ancho de
banda, como las videoconferencias.
MEO: Medium Earth Orbit
Órbita circular intermedia, entre 2.000 y 36.000 Km de
distancia de la superficie terrestre, con un período orbital promedio de varias
horas (12 horas en promedio)
Un tipo especial de órbita intermedia es la órbita Molnya,
especialmente usada por los países cercanos al círculo polar ártico. Esta
órbita desarrollada por Rusia, es altamente elíptica y muy inclinada, de modo
tener alta visibilidad desde las zonas polares.
La ventaja de ésta órbita es que permite a los países
nórdicos establecer satélites de comunicaciones para las regiones donde los
geoestacionarios no pueden llegar.
Principales aplicaciones: principalmente sistemas de
navegación de superficie estilo GPS., satélites de observación, defensa y posicionamiento.
GEO: Geoestationary Orbit
Es quizás la más conocida de todas: la órbita
geoestacionaria. Esta órbita ecuatorial se ubica a 35.786 km de la superficie
terrestre y tiene un período orbital de exactamente 23,93446 horas
(coincidiendo con la duración del día sideral), lo que hace que los satélites
puestos en esa órbita parezcan "inmóviles" en el espacio, ya que
rotan con la misma velocidad angular que la tierra.
Principales aplicaciones: esta órbita es el lugar donde se
ubican todos los satélites que proveen internet, televisión, telefonía y datos
a distintas regiones del globo, meteorología y operaciones de inteligencia.
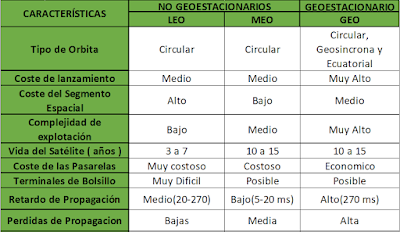
A continuación, se presenta un cuadro comparativo para
visualizar de una manera más eficaz las características de los sistemas
orbitales LEO, MEO, GEO:
2) Investigue que son los sistemas denominados SBAS
Los Sistemas de Aumentación Basados en Satélites (SBAS por sus siglas en inglés) son sistemas que proporcionan correcciones a las señales de los Sistemas Globales de Navegación por Satélite (GNSS) para mejorar la estimación en el cálculo de la posición geográfica, además de que ofrecen mayor integridad y disponibilidad de las señales de navegación, con lo que garantizan su empleo en aplicaciones críticas como la navegación aérea, en donde no se pueden permitir interrupciones en el servicio, como puede ocurrir con los sistemas GNSS como por ejemplo, cuando no se tienen por lo menos 4 satélites a la vista del receptor.
En el mundo existen varios sistemas de aumentación basados en satélite, entre los que sobresalen el WAAS de Norteamérica, el EGNOS de la comunidad europea, el SDCM de Rusia, y el MSAS de Japón. Asimismo, India está construyendo el suyo propio, denominado GAGAN.
3) Calcule la velocidad en el apogeo y en el perigeo para una orbita elíptica, con una
excentricidad igual a 0.667293983 y un semieje mayor 6500 km < a < 15000 km. cada 500
km.
excentricidad igual a 0.667293983 y un semieje mayor 6500 km < a < 15000 km. cada 500
km.
4) Calcule el periodo y la velocidad de una órbita circular, considerando los datos
del problema anterior (semieje mayor 6500 km < a < 15000 km. Cada 500 km.)
del problema anterior (semieje mayor 6500 km < a < 15000 km. Cada 500 km.)
Bibliografía